The linear algebra of Page-Rank
Published:
The linear algebra of google Page-Rank algorithm is essentially a fixed point formula. Let me sketch how it works. This is an interesting application of linear algebra, graph theory and probability.
A paradox principle
A website is important if it is linked by important websites.
A toy example
assume we have a small Internet consisting of just 4 web sites www.page1.com, www.page2.com, www.page3.com, www.page4.com, referencing each other in the manner suggested by the following diagram
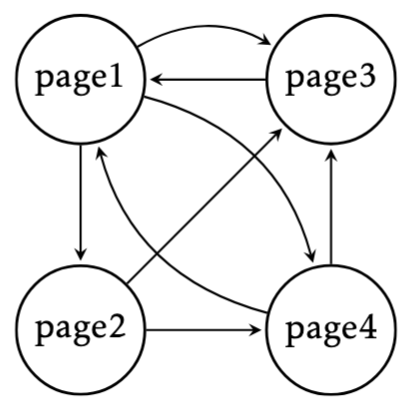
where the arrows/edges correspond to outgoing links: so that there is a link to page2 inside page1, whereas there is no link to page1 inside page2 and so on.
Let us denote by \(x_1\) the importance of page1 and similarly for \(x_2,x_3,4\). We look for the relative importance of the pages: we expect \(x_i\in [0,1]\) and \(x_1+x_2+x_3+x_4=1\). In our model, each page should transfer evenly its importance to the pages that it links to. For instance, \(page1\) has $3$ outgoing (blue) edges, so it will pass on \(1/3\) of its importance to each of the other \(3\) nodes. Let us label the arrows as follows (the color of the arrow is that of the source page)
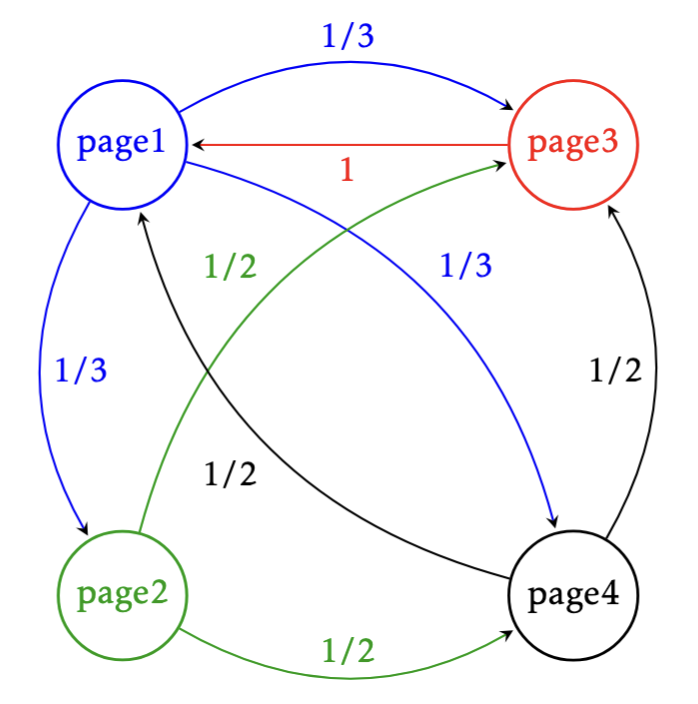
Now we can express the importance of the pages with the following equations
\[\begin{align} x_1&=0\cdot x_1+0\cdot x_2+1\cdot x_3+\frac{1}{2}\cdot x_4\\ x_2&=\frac{1}{3}\cdot x_1+0\cdot x_2+0\cdot x_3+0\cdot x_4\\ x_3&=\frac{1}{3}\cdot x_1+\frac{1}{2}\cdot x_2+0\cdot x_3+\frac{1}{2}\cdot x_4\\ x_4&=\frac{1}{3}\cdot x_1+\frac{1}{2}\cdot x_2+0\cdot x_3+0\cdot x_4 \end{align}\]which can be written in matrix form as a fixed point formula \(A\cdot \vec u = \vec u\), where
\[A=\begin{pmatrix}0 & 0 & 1 & 1/2\\ 1/3 & 0& 0 &0 \\ 1/3 & 1/2 &0 &1/2\\ 1/3 & 1/2 & 0 & 0\end{pmatrix} \ , \ \vec u=\begin{pmatrix} &x_1& \\ &x_2& \\ &x_3& \\ &x_4&\end{pmatrix}\ .\]Note that the columns of the matrix \(A\) are \emph{probability vectors}: i.e. vectors with non-negative entries whose sum is \(1\).
The Page Rank vector is the solution of this system which is a probability vector.
Note that the matrix of the system we want to solve is not \(A\), since we want all variables on the same side (infact we want to find the eigenspace relative to \(1\) of the matrix \(A\)). The matrix we need to use is
\[G=A-I=\begin{pmatrix}-1 & 0 & 1 & 1/2\\ 1/3 & -1& 0 &0 \\ 1/3 & 1/2 &-1 &1/2\\ 1/3 & 1/2 & 0 & -1\end{pmatrix} \ .\]By Gauss elimination, we get that this matrix has rank \(3\) and the nullity is one (so we just need one parameter, named \(c\) in the following). The solutions are the vectors
\[\vec u =\begin{pmatrix}12 c \\ 4 c \\ 9 c\\ 6 c\end{pmatrix}\ , \ c\in \mathbf{R}\ \text{parameter}\]which is a probability vector only for \(c=1/31\), since \(12+4+9+6=31\). Thus the Page Rank vector is
\[\vec r=\frac{1}{31}\begin{pmatrix}12 \\ 4 \\ 9 \\ 6 \end{pmatrix}=\begin{pmatrix}0.38 \\ 0.12 \\ 0.29 \\ 0.19\end{pmatrix}\]expressing the relative importance of the pages.
The toy example is too naive
In general such an \(A\) is called the transition (or adjacence) matrix associated to the graph. The matrix \(G=A-I\) is the Google matrix and \(\vec r\) is he Page Rank vector. All columns of \(A\) are probability vectors, matrices with this property are called stochastic matrices (Stochastic comes form from Greek \(\sigma\tau \acute o\chi o \zeta\) (stókhos), meaning aim, guess)
The problem is that the above method works only when the Google matrix \(G\) is of size \(n\) and rank \(n-1\):
in this case the set of solutions is a line (only one parameter) and we have only one probability vector on this line. This only happens for particular web graphs.
The Perron-Frobenius theorem states that if \(A\) is stochastic matrix with positive entries (all \(>0\)), then the equation \(A\vec u = \vec u\) has only one and only one probability vector solution.
For this reason, Brin and Page modified the adjacency matrix as follows
\[M:=(1-d)A+d S\ , \quad S=(1/n)_{n\times n} \ , \quad d=0.15\]where all entries of \(S\) are equal to \(1/n\) and \(d\) is called the damping factor. This is very clever and pragmatic. Such an \(M\) satisfies the Frobenius-Perron hypothesis for any initial web graph.
